Memetic Index - Memetic Glossary
Introduction
We need to start thinking about systems of agents who make deployment decisions and move a system forward. We need to start thinking about whether those systems converge into certain pathways and whether that resembles a stable society. We need to think about things such as mutation.
We need to start digging into the idea of endomemetic systems, and their mutation into idiomemetic systems, and these governing the deployment decisions of individual agents.
What I propose is a chess board, a chess game, where every piece is making its own decisions as to which moves it will make, and like in a real society, somebody gets picked to move (1). This brings us to the idea of how agents make decisions, and how agents vie with one another to decide which of them will deploy which memes. In other words, we must grapple with questions of deployment decisions (8).
A Simple Model
An easy way to generate moves in a game is to poll the pieces, select one of them, and have that piece return a move. The easiest way to select a move is to select evenly across all the pieces which are capable of moving, or, in algebraic chess notation, all of the movies which are able to be made by the given color whose turn it is (3). So we need a function to generate an array of moves. For example, the set of opening moves for white is:
[ [ a-h ][ 3, 4 ], N[ a, c, f, h ]3 ]
fig. 1a. All possible white opening moves (pawns, knights) (5)
Here's what these moves look like on an actual board.
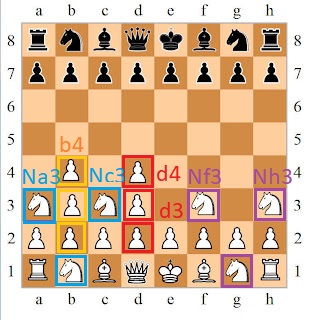 |
| fig. 1b. possible chess openings (not all pawn moves shows) |
Each move. is a meme that takes us to a new state, which is the configuration of the next board. Furthermore, that new state is now the point of departure for the next state, which we reach by the next move. Obviously, there are millions of states, but notationally we can represent it as "StateNow" or "StateX" or "State2" or whatever. For example, using algebraic chess notation, we can represent a knight moving for white with:
SetUp.Nc3! => QueenKnightOpen
fig. 1c. Notation for a chess move making a state transition
This highlights what we hope to accomplish in this essay. We can represent the possible opening as a state transition diagram, "SetUp", with all of the agents, that is, all eight pawns and the two knights.
| States / agents | QKO1 | Queen Knight Open | King Knight Open | KKO1 | PaOut | PbOut | PcOut | PdOut | PeOut | PfOut | PgOut | PhOut |
| queen-knight | Na3 | Nc3 | ||||||||||
| king-knight | Nf3 | Nh3 | ||||||||||
| pawns | a3, a4 | b3, b4 | c3, c4 | d3, d4 | e3, e4 | f3, f4 | g3, g4 | f3, f4 |
fig. 1d. Transition Matrix for opening chess moves (6) for state "SetUp"
The matrix gets pretty big if you include all the pawn moves separately (7). When describing a memetic system, using deployment descriptors is a good way to help verify the completeness and correctness of a memetic system outline. Here, until in fig. 1a., the pieces are explicitly mentioned and treated as agents. I've given distinct names to the pawn opening states as well.
fig. 1e. Deployment descriptors of all possible chess openings
This is not necessarily a good way to play a good game of chess, but it's more of a representation of how a community processes memes. If a learning system could be built in, it might be, however. In a subsequent version of the "selfish chess board," I may want to add features that are in addition to the moves themselves. Perhaps the pieces could "yell at" or "holler at" one another, and the pieces could react to these actions. All pieces still want to play, to win, and presumably to avoid being taken. Actually, all these priorities are up in the air. What kinds of attitudes of pieces will result in their color winning?
Once more with this "hollering" thing. If a piece can take memetic action that can potentially influence the states of other pieces, either on his own side or the other side, then that starts to make for a more interesting game. Is it useful to assume that all "hollers" are broadcast, or can they be monocast to a single piece or group of pieces (telephone gossip). So we "holler!(message)" and "gossip!(message, [ agent-list ] )" that can change the state of the board, even though no move has been made. Should these kinds of messages be "bosonic", that is, able to happen simultaneiously, as opposed to moves which only happen one at a time, in sequence?
_____________________
Bibliography
模倣子 Memetic State Diagrams and Transition Matrices
_____________________
Footnotes
(1) I just had a thought about how pieces decide which moves they themselves can make, like a pawn can decide, in the simplest, most unsophisticated way of choosing might be 50% to move forward one square and 50% to move ahead two. So playing like a child who only knows the moves and not strategy, say, one of the eight pawns or one of the two knights each gets 10% change of moving. So if one of them gets picked, the knights go either forward and left 50% or right 50% and the pawns ahead one or two, 50% each. Okay, first thing is that there is no accommodation for "don't move at all." Also, there's no accommodation for communication between agents.
The thought is that each agent could know their own possible moves, but also accommodate the possible moves of other agents. Like a pawn could decide to move only if the bishop and the queen decline to move, something like that. This involves some kind of communication or keeping track of the other players. This would suggest that the state, i.e., disposition of the players, maps directly onto a propensity to deploy a meme (make a move). Anyway, this is all a system to be worked out. I think what I'm looking for is making black boxes for all the pieces, and the inner decision process starts out as just stupidly dividing up the possible moves with equal probability, and advancing up to something more advanced, like an endomemetic model which may involve other pieces. There there's mutation (2).
(2) How to implement mutation in the endomemetic (idiomemetic) models? One possibility is whenever a piece "plans" to make a move but doesn't get "picked" there could be residual memetic debt which disfavors the given move, for example. Or there could be "collisions" that would be sorted out to reach a final decision. Or it could be random.
(3) Ultimately, we want a model that allows for mutation and learning (2). Whatever AI mechanism we give each piece, we'd like it either to mutate or replicate itself (4) or other such so that the system learns.
(4) One wild idea is that every time the piece moves, it makes a copy of its brain in a pool of cloned and mutated copies, every time it takes another piece it could make more copies, and when the piece is taken itself, whichever copy is "driving" is culled from the pool. Something like that.
(5) The knights and the pawns are moving to the same spaces, but no additional symbols are required to resolve ambiguity, like using the rank of to differentiate which is the one to move to either a3, c3, f3, or h3, since they are different pieces.
(6) Note that the axes are of the transition matrix are the available states and the agents who are able to deploy memes in that state. In this case all eight pawns and both knights are able to deploy memes, each of them having two choices (knights go right or left, and pawns forward one or two spaces). I have not given every pawn his own row, and I have not put two separate states for each pawn move, just for space and simplicity. The "name" of the matrix is the name of the state, hence this matrix is the "SetUp" matrix, and there is a "QueenKnightOpen" matrix, and a matrix for every other possible other move, and each of those is what the black player has to work with.
(7) The chess algebraic notation shortens the moves for pawns. While a knight moving out to space a3 is denoted Na3, while the pawn moving to the same space is just a3. It seems that the pawn is the "not otherwise specified" piece.
(8) Deployment decision is the still very much open area of Macromemetics dealing with how which agents decide to deploy which memes and not others. In the Triangular Baseball model, the ball, sometimes randomly, lands with a given player (agent) and then this agent has choices as to which meme to deploy, but it's relatively free of "jinx events" (9) and maybe also free of race conditions, depending upon the details of how the modeling is done. In chess, among the pieces, we have much possibility for jinx events. No race conditions, thanks to turn-taking (which is an issue in triangular baseball). One problem with deployment decision analysis is that there is currently no natural model for it. For a thought experiment like chess or triangle baseball you can pick a system based on random variables, genetic algorithms, probability tables, or whatever, and it might even produce something that looks like some observable reality, but that doesn't mean that it actually matches some kind of real memetic phenomenon. Getting to that will ultimately require some kind of medical and sociological research, I imagine.
(9) A jinx event is where two agents try to deploy memes at the same time. How does one decide which one takes precedence, whether they both retreat, or what?
No comments:
Post a Comment